Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов
Учим химию / Учим химию / Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов
Страница 4

При очень большом числе, факториал которого вычисляется, точной становится формула Стирлинга (можете проверить прямыми вычислениями). Разность между точным и приближённым логарифмами становится относительно малой величиной:

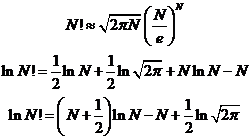
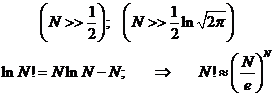
Таблица. Точные и приближённые значения логарифмов факториалов больших чисел.

N

N! точно

ln(N!)

точно

Стирлинг

точно

Стирлинг

прибл.

8

40320

10.604

10.594

8.635

9

362880

12.802

12.7925

10.775

10

3628800

15.1044

15.096

13.026

11

39916800

17.5023

17.4948

15.377

12

479001600

19.987

19.979

17.818

13

6227020800

22.55216

22.545

20.344

14

8.71782912*1010

25. 19122

25.185

22.947

20

2.432902008*1018

42.3356

42.33145

39.915

25

1.55112100*1025

58.00

57.998

55.470

50

3.041409*1064

148.478

148.476

145.601

ПРИЛОЖЕНИЕ 2.

Дополнительные сведения о вращательных статистических суммах.

Для справки приведём ротационные статистические суммы молекулы с учётом её внутренних вращений

Суммы по состояниям для внутреннего вращения (Ерёмин, стр.181-182):

Страницы: 1 2 3 4 5

Смотрите также

Задание
1.    Уравнение реакции         Br                                                                   Br ...

Принципы определения примесей арсена в неизвестном минерале
В условиях активного загрязнения окружающей среды и реальности экологического кризиса возрастает значение научных исследований, направленных на изучение состояния экосистемы, и практического ...

Дмитрий Иванович Менделеев
...