Это и есть основание для расчёта константы химического равновесия.

Применяя правило ИЮПАК для стехиометрических коэффициентов, формулу (21.3) легко записать в общем виде

; (5)

Введём стандартные химические потенциалы веществ i.

. (6)

Стандартное сродство реакции принимает вид

; (7)

Сокращая на RT=NkT, получаем

; (8)

Константа химического равновесия в смеси идеальных газов.

Совершим цепочку несложных преобразований. Вначале внесём стехиометрические коэффициенты в сумме под знак логарифма в виде показателей степеней у статистических сумм

; (9)

Затем воспользуемся тем, что сумма логарифмов равна логарифму произведения

; (10)

Наконец, избавляясь от логарифмов, получаем искомое статистическое выражение для константы равновесия

; (11)

Она имеет вид произведения статистических сумм.

Константа химического равновесия в смеси идеальных газов.

; (12)

Стандартные суммы состояний имеют вид:

- трансляционная: 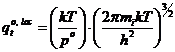; (13)

- молекулярная: 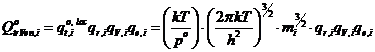; (14)

Константа равновесия может рассчитываться как непосредственно в виде произведения статистических сумм,

; (15)

которые предварительно следует рассчитать, а также по результирующей формуле

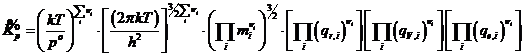; (21.14)

При вычислении электронных сумм состояния помним, что занят один-единственный электронный уровень, и он характеризуется кратностью вырождения ge, i. Эта кратность равна числу микросостояний основного терма у атомов и у молекул. У молекул чаще всего достаточно спиновой мультиплетности, но возможно и орбитальное вырождение. Это уже зависит от конкретной частицы.

Поэтому электронная сумма состояний у молекулы определяется формулой

; (16)

Энергия химической связи считается равной энергии её диссоциации и отсчитывается от основного колебательного уровня, а не от минимума потенциальной кривой.

Этот вопрос рассмотрен в учебнике Даниэльса и Олберти на стр.539 в разделе 17.13. Там же приводятся основные формулы. Раздел написан хорошо и достаточно просто. Этот учебник вполне пригоден для подготовки студентов.

1. Сводка статистических сумм для простейших стационарных движений.

ПРИЛОЖЕНИЕ 1. Математическая справка о факториалах больших числах.

Факториал числа, соизмеримого с числом Авогадро, непосредственно вычислить невозможно, и поэтому давно разработаны приближённые способы численно точного вычисления, основанные на применении гамма – функции Эйлера первого рода.