Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов
Учим химию / Учим химию / Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов Химическая реакция в смеси идеальных газов. Константа химического равновесия в смеси идеальных газов
Страница 5

Для свободного внутреннего вращения в этане (при высокой температуре):

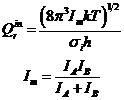
Для каждой из двух свободно вращающихся групп в сложной молекуле:

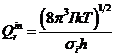
Число молекулярной вращательной симметрии требует специального анализа. Там же у Ерёмина приводятся приёмы расчёта.

Учитывая все ротационные преобразования симметрии, например, для этана получаем число 18 (3 степени свободы для вращения вокруг оси 3-го порядка вдоль связи C-C, ещё 2 - для оси 2-го порядка и также для внутреннего вращения – вновь ось 3-го порядка).

Вся ротационная сумма состояний в общем случае приобретает вид:

(Ерёмин, стр.233, формула VI.155)

.

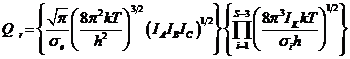Множитель p1/2 появляется при вычислении ротационной статистической суммы методом классической статистики, тогда как вывод общей формулы на основе квантовой статистики невозможен.

Вращательные стат. суммы сложных молекул и ротационное число симметрии.

(см. Приложение – несколько страниц из книги Дж. Майер, М. Гёпперт-Майер).

Страницы: 1 2 3 4 5 

Смотрите также

Гранулированная форма хитозана. Получение и свойства
Уникальные свойства хитина и хитозана привлекают внимание большого числа специалистов самых разных специальностей. Роль полимеров в нашей жизни является общепризнанной, и все области их при ...

Эпитаксиальный рост Ge на поверхности Si(100)
С физикой тонких пленок связаны достижения и перспективы дальнейшего развития микроэлектроники, оптики, приборостроения и других отраслей новой техники. Успехи микроминиатюризации электронн ...

Галогены
Галогены (солероды) – фтор F,  хлор Cl ,  бром Br,  йод I и астат At расположены в главной подгруппе VII группы периодической системы элементов Д.И.Менделеева. Все галогены, кроме астата, вст ...