Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Связи м/у активностями компонентовСтатьи и работы по химии / Активность. Порядок реакций / Статьи и работы по химии / Активность. Порядок реакций / Связи м/у активностями компонентов Связи м/у активностями компонентов
Уравнение Дюгема-Маргулиса:
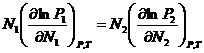(1). Если раствор является близким к совершенному, то 
, а 
. 
, 
. Продифиринцируем (
и 
=const) 
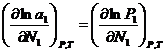(2), 
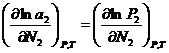(3). Подставим 
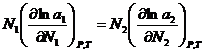(4). Уравнение (4) может быть обобщено на раствор, содержащий несколько компонентов: 
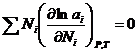. Если раствор близок к разбавленному 
для растворённого вещ-ва 
. Повторяя действие, что и здесь справедливо уравнение (4). Для бинарного раствора уравнение (4) имеет вид: 
, 
, 
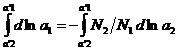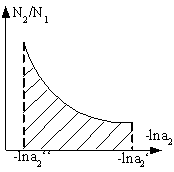
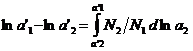. Если известна зависимость активности второго компонента от концентрации, а так же активность первого компонента для какой либо концентрации, то можно активность компонента для другой концентрации. Зная 
, можно подсчитать 
.
Смотрите также
Магнийорганические соединения
Магнийорганические
соединения относятся к числу одних из самых известных металлоорганических соединений.
Они широко применяются в органическом синтезе, хотя в последнее время их
потеснили л ...
Важнейшие представители ароматических аминов
Анилин впервые был получен в результате перегонки индиго с известью
(1826г.). В 1842 г. его получил Зинин восстановлением нитробензола. В
незначительных количествах содержится в каменноугольной смол ...