Операторы момента импульса и их коммутация

Вместе с модулем момента импульса , или эквивалентно , квантуется и направление этой векторной величины, но в довольно своеобразной форме, отличной от классического представления о направлении векторов. Исследуем это квантование по направлению.

4.3.5.1. Как следует из раздела 4.3.4.4, наряду с , функции отвечает совершенно определенное значение , но две другие проекции и остаются неопределенными. Это не случайно, а обусловлено принципом неопределенности Гейзенберга. Легко убедиться в этом, показав, что не коммутирует с и , но в то же время коммутирует с. Аналогично между собой не коммутирует любая пара из .

В качестве примера найдем коммутатор

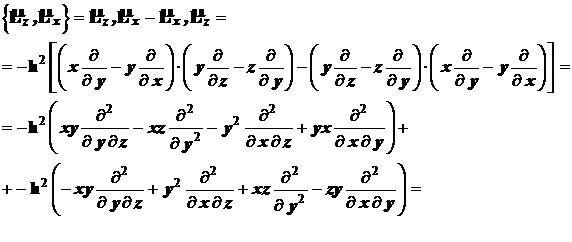
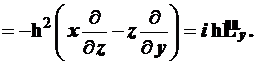(4.65)

Аналогично можно получить следующие соотношения

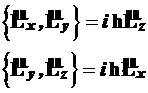(4.66)

4.3.5.2. Эти формулы полезны для отыскания возможных значений квадрата момента импульса и волновых функций при решении уравнения (4.62), которое несомненно сложнее решения (4.63). Для разрешения этой задачи воспользуемся приёмом, ранее примененным нами для гармонического осциллятора (см. раздел 3.51) когда собственные значения и собственные функции оператора Гамильтона были найдены лишь на основе коммутационных соотношений, а также операторов сдвигов состояний.

4.3.5.3. Сконструировав специально операторы сдвига состояний, можно решить и задачу о вращательных состояниях жесткого ротатора. В этом случае мы будем перемещаться от состояния к состоянию с одним и тем же значением , а, следовательно, и с одной и той же кинетической вращательной энергией, т.е. внутри вырожденного уровня попытаемся "пересчитать" дискретные состояния. Они отличаются только значениями , т.е. ориентациями вектора момента импульса. Главная проблема на данном этапе – отыскание квантового числа l, квантующего модуль вектора

4.3.5.4. Для этой цели запишем, как обычно

(4.67)

и одновременно учтём, что справедливы операторные уравнения

(4.68)

(4.69)

Вместе с тем, как и в теории плоского ротатора

(4.70)

Вычтем почленно (4.70) из (4.68) и получим

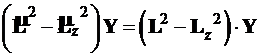,(4.71)

а с учётом (4.67)

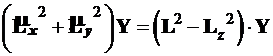(4.72)

Таким образом, функция Y оказывается собственной функцией оператора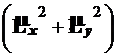, т.е.

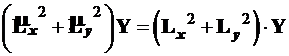(4.75)

где – собственное значение.

В силу самосопряженности операторов квантовой механики, их собственные значения должны быть вещественными и единая физическая величина как сумма квадратов может быть только положительной. Это справедливо, несмотря на недоступность для индивидуального определения каждого из слагаемых и

Из сопоставления (4.72) и (4.73) следует неравенство

(4.74)

Отсюда . (4.75)

4.3.5.5. Формула (4.75) содержит прозрачный смысл: квадрат момента импульса не может быть меньше квадрата одной из его проекций. Одно и то же значение модуля момента импульса, определяемое квантовым числом l, может отвечать состояниям с различными значениями проекции , которые задаются квантовым числом m. При этом каждому состоянию с положительным значением m соответствует состояние с отрицательным m, отличающееся направлением вращения вокруг оси z. Формула (4.75) одновременно определяет пределы изменения квантового числа m, увязывая его с числом l в виде