Оптимальный вариант состоит в подборе таких валентных потенциалов, жёсткость которых мало отличается от невалентных. Один из них, известный как потенциал FENE, имеет вид

-k´r02 ln[1-(r/r0)] при r < r0

Uij(r) = (2.4)

2. при r > r0

Здесь r

–

расстояние между парой связанных частиц

i

и j

, а параметры k

и r

0

принимаются равными 10e/s2 и 1.95s. Другой удачной аппроксимацией является конструкция из двух потенциалов Леннарда-Джонса, действующих навстречу друг к другу и описывающих только отталкивание.

e0[(b/r)12 – 2(b/r)6 +1 при r < b

Uij(r) = (2.5)

e0 b12 _ 2b6 +1 при r > b

(2b-r)12 (2b-r)6

Здесь b

–

заданная длина связи между частицами i

и j

.

Данная функция имеет нулевой минимум при r

=

b

и становится бесконечной при r

= 0 и r= 2b

.

3. Энергия деформации углов.

Для каждого атома в молекуле существуют некоторые идеальные углы, отклонение от которых требуют затрат энергии угловых деформаций (Еугл). Предполагается, что эта энергия аддитивна, причём при малых отклонениях справедлив закон Гука. Аналогично энергии деформации связей можно записать.

U(q) = C´(qi - q)2 (2.6)

Где С – силовая константа,

q- идеальное значение угла связи,

qi – мгновенное значение угла связи

Деформация углов происходит значительно легче, чем деформация связей ( константа К на порядок выше, чем С).

Для описания угловых напряжений можно использовать потенциал (2.5), если в качестве параметра b

взять расстояние между атомами, разделенными двумя связями.

4. Невалентные взаимодействия атомов (Ес).

Рис.2.1 Общий вид потенциальной функции невалентных взаимодействий.

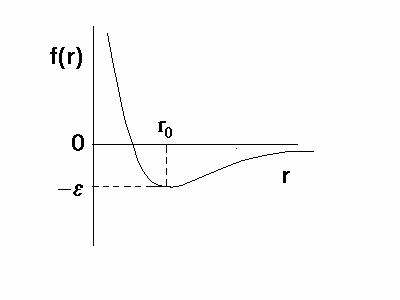
В попарно аддитивном приближении стерический вклад в потенциальную энергию молекулы выражается через взаимодействия отдельных атомов[10].

Ec = ååfij(r) (2.7)

i < j

Взаимодействия валентно не связанных атомов складывается из дисперсионного (а также индукционного и ориентационного) притяжения и отталкивания, возникающего из-за перекрывания электронных оболочек на малых расстояниях. На рис. 2.1 показана потенциальная функция f(r) взаимодействия двух атомов в зависимости от расстояния r

между ними.

Отталкивание между атомами апроксимируется обычно функциями вида B

/

rnили Cexp

(-

Dr

), а притяжение – функцией A

/

rm

(A, B, C, D, m, n – постоянные).

Отсутствие строгого выражения для f

(

r

)

вынуждает искать приближённые аналитические формы. Наибольшее распространение получили потенциалы типа "6-12" и "6 - exp".

Потенциал Леннарда – Джонса (

m

–

n

)

f(r) = ne(n-m)-1(n/m)m/(n-m)[(s/r)n – (s/r)m] =

ne(n-m) –1[(m/n)(r0/r)n – (r0/r)m],

где r

0= 21/6´s, m и n – численные коэффициенты. Коэффициент m выбирается равным 6. Величина n лежит в интервале от 10 до 14 и чаще всего принимается равной 12.