Существует две группы способов получения дисперсных систем:

7. Способы диспергирования

заключаются в раздроблении тела до коллоидного состояния (мукомольное производство).

8. Способы конденсации

заключаются в укрупнении частиц, атомов, молекул до частиц коллоидных размеров (химическая реакция с образованием осадка).

Молекулярно-кинетические свойства дисперсных систем

Все молекулярно-кинетическиесвойства вызваны хаотическим тепловым движением молекул дисперсионной среды, которое складывается из поступательного, вращательного и колебательного движения молекул.

Молекулы жидкой и газообразной дисперсионной среды находятся в постоянном движении и сталкиваются между собой. Среднее расстояние, проходимое молекулой до столкновения с соседней, называют средней длиной свободного пробега. Молекулы обладают различной кинетической энергией. При данной температуре среднее значение кинетической энергии молекул остается постоянным, составляя для одной молекулы и одного моля:

; ,

где m – масса одной молекулы;

M – масса одного моля;

v – скорость движения молекул;

k – константа Больцмана;

R – универсальная газовая постоянная.

Флуктуация значений кинетической энергии молекул дисперсионной среды (т.е. отклонение от среднего) и является причиной молекулярно-кинетических свойств.

Изучение молекулярно-кинетических свойств возможно в результате применения статистических методов исследования, действительных для систем, состоящих из множества элементов (молекул). Исходя из допущения о беспорядочности движения отдельных молекул, теория определяет наиболее вероятное сочетание для систем из множества объектов. Молекулярно-кинетические свойства проявляются в жидкой и газообразной среде, молекулы которых обладают определенно подвижностью.

Броуновское движение

Броуновским называют непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц, взвешенных в жидкостях или газах, за счет воздействия молекул дисперсионной среды.

Мельчайшие частицы незначительной массы испытывают неодинаковые удары со стороны молекул дисперсионной среды, возникает сила, движущая частицу, направление и импульс силы, непрерывно меняются, поэтому частица совершает хаотические движения.

F

х

Определили эти изменения и связали их с молекулярно-кинетическими свойствами среды в 1907 году А. Эйнштейн и М. Смолуховский. В основе расчета – не истинный путь частицы дисперсной фазы, а сдвиг частиц. Если путь частицы определяется ломаной линией, то сдвиг х характеризует изменение координат частицы за определенный отрезок времени. Средний сдвиг определяет среднеквадратичное смещение частицы:

,

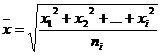где х1, х2, хi – сдвиг частиц за определенное время.

Теория броуновского движения исходит из представления о взаимодействии случайной силы f(t), характеризующей удары молекул, силы Ft, зависящей от времени, и силы трения при движении частиц дисперсной фазы в дисперсионной среде со скоростью v. Уравнение броуровского движения (уравнение Ланжевена) имеет вид: , где m – масса частицы; h - коэффициент вязкости дисперсионной среды. Для больших промежутков времени (t>>m/h) инерцией частиц (m(dv/dt) можно пренебречь. После интегрирования уравнения 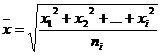при условии, что среднее произведение импульсов случайной силы равно нулю, среднее значение флуктуации (средний сдвиг) равно: 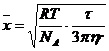, где t - время; r – радиус частиц дисперсной фазы; NA – число Авогадро частиц.

В этой формуле характеризует молекулярно-кинетические свойства дисперсионной среды, h - ее вязкость, r – радиус частиц – параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой.

Кроме поступательного, возможно вращательное броуновское движение для двухмерных частиц и частиц неправильной формы (нитей, волокон, хлопьев и т.д.).