В основе квантовой механики лежит уравнение Шредингера, играющее в ней такую же важную роль, как и уравнения Ньютона в классической механике. Также как и уравнения Ньютона, уравнение Шредингера не выведено ни из какой физической теории, а является постулатом, полученным в результате обобщения опытных фактов.

Для совокупности N взаимодействующих частиц с потенциальной энергией U и массами mk в декартовой системе координат оно имеет вид

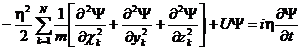
где Ψ(x, y, z, t) – волновая функция совокупности координат системы частиц и времени, U – оператор потенциальной энергии. Суммирование производится по всем частицам.

Стационарные состояния удовлетворяют не зависящему от времени уравнению Шредингера:

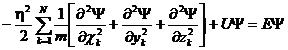
Параметр Е есть собственное значение стационарного уравнения Шредингера. В результате решения стационарного уравнения Шредингера находят собственные (возможные) значения параметра Е и соответствующие ему решения – собственные функции.

Для любого уравнения Шредингера, соответствующего конкретной системе, существует бесконечное множество значений параметра Е. Эти значения могут быть как непрерывными (для свободно движущейся частицы), так и дискретными, если частицы локализованы в малой области пространства. Дискретные значения Е называют уровнями энергии.

Пользуясь операторной символикой, можно записать уравнение Шредингера в сокращенной форме:

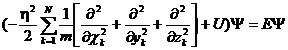
ĤΨ = ЕΨ,

где Ĥ = 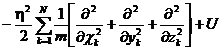- оператор Гамильтона или гамильтониан системы частиц.

1970 - 1980-е годы были временем очень быстрого развития вычислительных методов квантовой химии. В результате появилась возможность рассчитывать геометрию и оценивать стабильность промежуточных продуктов и переходных состояний, а также вычислять профили поверхности потенциальной энергии вдоль координаты реакции. Экспериментальное получение подобной информации для большинства реакций связано с преодолением значительных трудностей, вызванных многостадийным характером процессов, синхронным протеканием отдельных элементарных стадий и очень малым временем жизни промежуточных продуктов. Развитие вычислительных методов квантовой химии и появление быстродействующих ЭВМ позволили рассчитывать многие характеристики органических соединений, в том числе и нестабильных, а также переходных состояний. Точность этих расчетов получается вполне удовлетворительной по термохимическим стандартам. Поэтому квантовохимические расчеты в настоящее время используются в качестве одного из физико-химических методов исследования для получения данных, необходимых для установления механизмов сложных органических реакций.

Существующие методы математического моделирования "структура- активность" могут быть условно разделены на три группы.

Первая группа основана на использовании принципа линейности свободных энергий и включает в себя такие подходы, как метод Хэнча, метод Кубиньи и "диффузионный подход".

К этой же группе причисляют аддитивно- статистические методы Фри - Уилсона, Фуйита - Бана, Каммарата - Яу и им подобные. Для построения моделей, реализующих принцип линейности свободных энергий, используются методы регрессионного анализа.

Вторая группа объединяет методы, предназначенные для получения первоначальных представлений об изучаемом явлении посредством статистической обработки всей имеющейся информации, а также преобразования ее к виду, удобному для дальнейшего использования. Эта группа методов иногда называется методами "генерации гипотез". Она объединяет такие методы, как факторный анализ во всех его модификациях, методы линейного отображения, иногда к этой группе относят и аддитивно- статистические методы.

В третью группу включают методы, основанные на использовании алгоритмов теории распознавания образов, предназначенные для классификации объектов посредством разнообразных статистических и эвристических процедур. К этой группе относят различные методы дискриминантного анализа, порогового логического элемента и его модификации, методы теории алгебры логики.