Подробный расчет теплообменного аппарата. Теплоотдача в трубах
Дипломы, курсовые и прочее / Процессы и аппараты химической технологии / Дипломы, курсовые и прочее / Процессы и аппараты химической технологии / Подробный расчет теплообменного аппарата. Теплоотдача в трубах Подробный расчет теплообменного аппарата. Теплоотдача в трубах

Находим, что теплоотдача для раствора описывается уравнением:

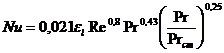, (3.25)

где - критерий Нуссельта; - поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля; - критерий Прандтля при температуре стенки трубы.

Коэффициент примем равным 1, полагая, что (/1/, табл. 4.3, стр. 153), где - длина труб, - эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле:

, (3.26)

где - средняя скорость потока, и - соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре .

По формуле 3.7 плотность раствора при и % масс. равняется:

,

.

Среднюю скорость потока определяем по формуле:

Учитывая, что для труб круглого сечения диаметр труб и эквивалентный диаметр совпадают, то для труб получаем:

.

Критерий Прандтля находим по формуле:

, (3.27)

где - удельная теплоемкость, ; - коэффициент теплопроводности, ; - динамический коэффициент вязкости, .

Коэффициент теплопроводности при и % масс. по формуле 3.15 равняется:

,

.

Таким образом, критерий Pr при и равняется:

Коэффициент теплоотдачи от раствора к стенке:

.

С учетом формулы 3.25 получаем:

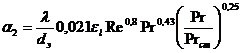, (3.28)

.

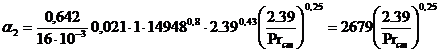Смотрите также

Обсуждение результатов
Таким образом, в предыдущих разделах рассмотрен материал, включающий различные методы получения гетероциклических соединений реакциями замыкания цикла, свойства, общую информацию, применение и полу ...

Химические преобразователи солнечной энергии
  Современная энергетика опирается главным образом на такие источники, в которых запасена солнечная энергия (СЭ). Прежде всего это ископаемые виды топлива, для образования которых требуются ...

Конструирование биосенсора для регистрации P. aeruginosa АТСС 27853
Регистрация патогенных микроорганизмов в растворах электролитов является одним из основных заданий медицины, биохимии и электрохимического анализа. С этой целью в мире разрабатываются биосе ...