Сопряжение - внутримолекулярное возмущение соседних атомных р-орбиталей. В непредельных углеводородах, содержащих соседствующие друг с другом, т.е. сопряженные, кратные (двойные или тройные) связи, π-орбитали кратных связей могут возмущаться путем бокового перекрывания. В результате образуется делокализованная π-система, орбитали которой охватывают всю сопряженную систему и называются молекулярными π-орбиталями. Это хорошо видно на рис. 1.22 (гл. 1), на котором изображены полученные с помощью ЭВМ объемные контуры π-орбиталей бутадиена. Сопряженные системы могут быть линейными или циклическими. Минимальные сопряженные системы состоят из трех р-орбиталей. К ним относятся аллильные и циклопропенильные катион, радикал и анион:

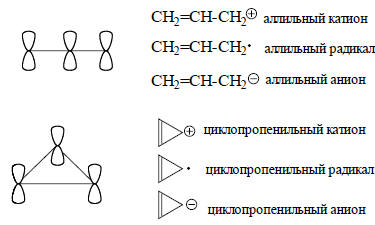
Четырехатомной π-системе соответствуют 1,3-бутадиен и циклобутадиен; к пятиатомной системе относятся пентадиенильные и циклопентадиенильные катион, радикал и анион; шестиатомные сопряженные системы - это 1,3,5-гексатриен, бензол, и т.д.:

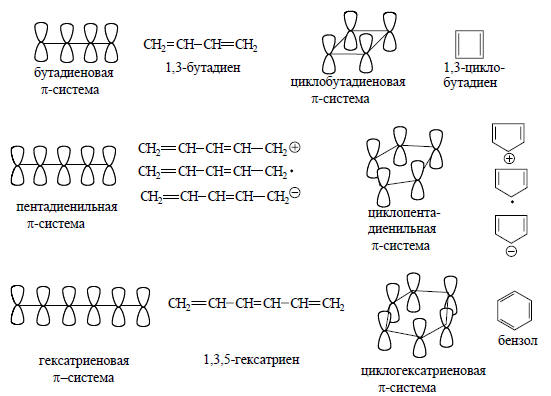
Очевидно, что нейтральные сопряженные углеводороды, в которых все атомы углерода четырехвалентны, содержат четное число атомов, имеющих р-орбитали. Нечетные сопряженные системы представляют собой или катион, или радикал, или анион, т.е. содержат трехкоординационный атом углерода.Простейшей π-системой является одиночная атомная р-орбиталь, например, в метильном катионе, радикале или анионе. Когда объединяются две р-орбитали, образуется этиленовая π-система, состоящая из связывающей и разрыхляющей орбиталей. Эти орбитали можно построить на основе теории возмущения, как показано на рис. 2.5 (ср. рис. 2.1).

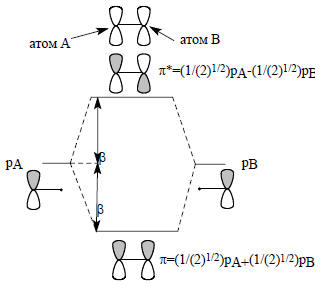Рис. 2.5. Представление молекулярных орбиталей через составляющие их атомные орбитали. Более реальная картина π-орбиталей этилена дана на рис. 1.19 (гл. 1).

Здесь взаимодействуют две С2р-орбитали одинаковой энергии, поэтому должно быть возмущение первого порядка, которое описывается уравнением (2.6). Орбиталь π имеет вид π=САрА+СВрВ, а орбиталь π*=СА*рА-СВ*рВ, где СА, СВ, СА* и СВ* - коэффициенты, с которыми входят орбитали рА и рВ в орбитали π и π*. Для нормализованных орбиталей, т.е. орбиталей, согласованных с принципом квантования (см. разд. 1.3, гл. 1), СА2+СВ2=1 и СА*2+СВ*2=1. Кроме того, СА2+СА*2=1 и СВ2+СВ*2=1. Поскольку возмущение первого порядка, рА и рВ вносят одинаковые вклады в π и π* и, следовательно, СА = СВ = СА*= СВ*= 1/2.По аналогии с молекулой этилена строятся π-МО простейших сопряженных систем - аллильной и циклопропенильной. Для этого рассматриваются возмущения, возникающие в системе при объединении двух орбиталей этилена (π и π*) и одиночной р-АО. Возмущения при образовании аллильной системы изображены на рис. 2.6.

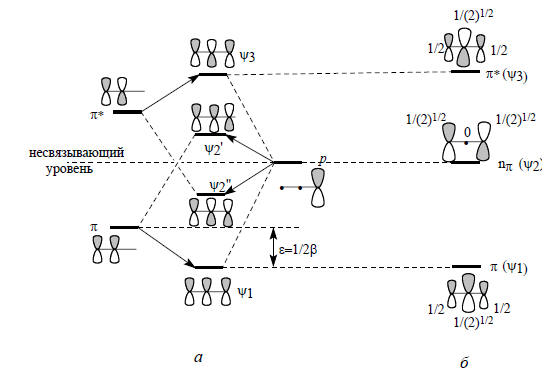Рис. 2.6. Этапы построения (а) и истинные (б) π-орбитали аллильного типа

В результате возмущения второго порядка π, взаимодействуя с орбиталью р, в фазе дает орбиталь ψ1, а в противофазе - орбиталь ψ2’. Орбиталь π*, взаимодействуя в орбиталью р, в фазе дает орбиталь ψ2’’ , а в противофазе - орбиталь ψ3.Внимание! На рис. 2.6,а из трех базисных орбиталей получилось четыре возмущенных, хотя возмущенных орбиталей тоже должно быть три. Эту ошибку легко исправить. Рассмотрим орбитали ψ2’ и ψ2’’. Несвязывающий уровень р под влиянием возмущения со стороны орбитали π этилена повысился (до ψ2’), а под влиянием возмущения со стороны орбитали π* понизился (до ψ2’’). Другими словами, уровни ψ2’ и ψ2’’ мы должны заменить одной несвязывающей орбиталью ψ2. Какова симметрия этой аллильной несвязывающей орбитали? Сравним диаграммы некорректных орбиталей ψ2’ и ψ2’’. Правые и левые р-АО-составляющие для обеих орбиталей выглядят одинаково, но средняя р-АО орбитали ψ2’ имеет относительные знаки верхней и нижней долей, противоположные относительным знакам верхней и нижней долей орбитали ψ2’’. Значит, несвязывающая аллильная орбиталь должна иметь нулевой вклад от центрального атома углерода, т.е. на диаграмме несвязывающей аллильной π-орбитали вклад центральной р-АО должен отсутствовать. Таким образом, три π-орбитали аллильной системы имеют симметрию, показанную на рис. 2.6, б.Из рисунка видно, что сопряжение понижает энергию π-электронов по сравнению с их энергией в изолированной двойной связи.Аллильная сопряженная π-система стабильнее (т.е. имеет более низкую энергию π-электронов) по сравнению с системой «изолированная этиленовая π-связь плюс изолированная р-орбиталь» за счет понижения энергии электронной пары на нижней π-орбитали ψ1. Обычно несвязывающие орбитали обозначают символом n; таким образом, аллильная π-система имеет три орбитали: π(ψ1), nπ(ψ2) и π*(ψ3).Энергию стабилизации аллильной π-системы можно вычислить, например, методом Хюккеля (гл.1,) или с помощью уравнения (2.8), в котором коэффициенты равны 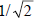(см. рис. 2.5) и 1 (для одиночной р-орбитали), а ΔЕα=β. Вычисления показывают, что орбиталь ψ1 имеет более низкую энергию по сравнению с π-орбиталью этилена (рис. 2.6) на величину ε=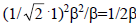, а поскольку эта орбиталь занята двумя электронами, энергия стабилизации будет равна β.Теперь рассмотрим коэффициенты, с которыми каждая из трех углеродных аллильных р-орбиталей входит в каждую из трех делокализованных аллильных π-орбиталей. Последние можно записать в следующем виде: ψ1 = С11ϕ1+ С12ϕ2+С13ϕ3 (разрыхляющая), ψ2 = С21ϕ1+ С22ϕ2+С23ϕ3 (несвязывающая), ψ3 = С31ϕ1+ С32ϕ2+С33ϕ3 (связывающая).Первая цифра индекса при коэффициенте С отражает порядковый номер орбитали ψi, а вторая - номер атома углерода в аллильной цепочке и номер его АО ϕi.Коэффициенты С для любой π-системы можно рассчитать по методу Хюккеля, однако для длинных π-систем этот расчет достаточно труден. Для сопряженных полиенов с открытой цепью Н(СН=СН)N/2Н, содержащих N атомов углерода, коэффициенты можно определить из уравнения Cij = [2/N+1]1/2sin[ijπ/(N+1)], (2.10), где - i - номер данной молекулярной орбитали (i=1 для самой нижней МО); j - положение данного атома в углеродной цепочке. Например, рассчитаем коэффициенты орбитали ψ2 аллильной π-системы: