(51)

Применительно к кинетике реакций с линейным механизмом величина х в линейном законе у = ах – концентрация i-того интермедиата, а – вес стадии , у – скорость стадии . Это правило было использовано по аналогии Волькенштейном и Гольдштейном для вывода кинетических уравнений скорости ферментативных реакций методом графов. В работах Яблонского и сотр. доказано соотношение (51), и показана его связь с правилом Крамера. Если и D записать через веса стадий, а в случае каталитической реакции вынести из концентрацию катализатора ([М], КГ5), получим:

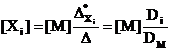, (52)

где Di = , DM = D

Из (50) и (52) получаем также

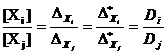(53)

В случае некаталитических реакций концентрация Xi запишется через концентрацию нуль-вещества в нуль-вершине графа

(54)

Если все [Xi] в каталитической реакции выразить через [М], получим выражение для суммарной концентрации катализатора

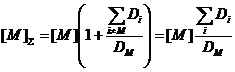(55)

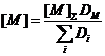(56)

Из (52) и (56) получаем

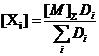(57)

В гетерогенных процессах при нормировке всех Xi к [Х]S (выражение [Xi] через доли поверхности ) получаем

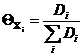(58)

Есть два способа учесть наличие висячих вершин в материальном балансе по катализатору. Найдя корневые определители для висячих вершин, их следует включить в , тогда [М]S будет включать и соединения, находящиеся в висячих вершинах. Поскольку ребра графа, инцидентные висячим вершинам, в случае стационарных и квазистационарных процессов являются равновесными стадиями, можно ввести дополнительную функцию – закомплексованность интермедиата (любой вершины циклического графа)

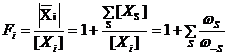(59)

где [XS] – концентрация соединения в висячей вершине графа, связанной с графом стадией S, wS и w–S – веса стадии, инцидентной висячей вершине и направленной от Xi к XS. Очевидно, что отношение включает константу равновесия KS и концентрации участников реакции, входящие в wS и w–S. Так, для вершины М в графе КГ4 получим

Формула (57) может быть модифицирована, поскольку ,

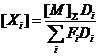(60)

По уравнению стационарности стадий легко установить связь скорости стадии со скоростью по маршруту, и таким образом найти RP. При отсутствии висячих вершин Fi = 1.

Другой алгоритм был предложен Волькенштейном и Гольдштейном и модифицирован Яблонским и сотрудниками. На графе многомаршрутной реакции выбирается стадия, принадлежащая одному из маршрутов (Wj = RP), и скорость этой стадии записывается уравнением (64)