(4.10)

Подставляя (4.9) и (4.10 ) в (4.8), получаем

(4.11)

Каждый из одномерных операторов дифференцирования преобразу­ет лишь ту функцию-сомножитель которая содержит его же аргумент. Остальные функции-сомножители без нарушения равносильности уравнения (4.11) можно вынести влево за такой оператор:

4.1.2.10 соответствии с методом Фурье, слева домножаем выражение на и получаем

Отделяя любое из слагаемых, например, первое, вводим первую из констант связывающих отдельные компоненты решения

и т.д.

(4.12)

4.1.2.11. Суммируя левые части уравнений системы (4.12) и все константы в правой части, получаем

т.е. или 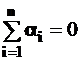(4.13)

Таким образом, параметры отдельных одномерных дифференциальных уравнений оказываются связанными между собой равенством (4.13).

4.1.2.12.При разделении переменных многомерного дифференци­ального уравнения можно их предварительно группировать. В таком случае в выражениях (4.8 ) – (4.10)под каждым из символов может подразумеваться целый набор переменных. Именно таким об­разом производится анализ движения в системе многих частиц. Внача­ле очень сложное и громоздкое исходное уравнение всегда претерпе­вает подготовительное преобразование, состоящее в том, что произ­водится выделение отдельных уравнений, относящихся к индивидуальным частицам.

4.1.2.13. Встречаются ситуации, когда, на первый взгляд, раз­делить переменные невозможно, так как оператор содержит слож­ные функции, включающие все эти переменные либо часть из них. В таких случаях часто к цели ведёт замена переменных, например, пе­реход от декартовых координат х, у к полярным или к комбинации исходных декартовых. Преобразования, связанные со сменой координат, и в классической и в квантовой механике являются самым обычным делом. Выбор подходящей системы переменных часто подсказывает выра­жение потенциальной энергии . Ниже мы встретимся с такими примерами.

4.1.2.14. Следует отметить, что простая аддитивная форма опе­ратора не является непременным условием разделения переменных в дифференциальном уравнении (4.8). Встречаются и более сложные конструкции операторов, допускающие возможность использования основных принципов решения дифференциальных уравнений в частных про­изводных по методу Фурье с разделением переменных. Ниже мы столкнемся с такими случаями.

Различным комбинациям квантовых чисел может отвечать одно и то же значение суммы квадратов В этом случае все такие состояния относятся к одному вырожденному уровню. Обозначим их число – кратность вырождения уровня – буквой g. На примере шести низших уровней кубического "ящика" проследим их вырождение . Для этого, как обычно, составим таблицу состояний и уровней (табл. 4. 1.) и изобразим энергетическую диаграмму этой системы ( рис. 4.1.).