Обработка результатов

Для малых выборок использовали распределение Стьюдента, которое связывает между собой ширину доверительного интервала, соответствующую ему вероятность и объем выборочной совокупности.

Для выборки в n результатов рассчитывали среднее

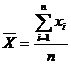
и дисперсию, характеризующую рассеяние результатов относительно среднего

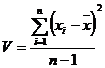
Для характеристики рассеяния результатов в выборочной совокупности использовали также стандартное отклонение

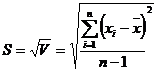
и относительное стандартное отклонение значений

Величину доверительного интервала измеряемой величины для заданной доверительной вероятности рассчитывали, пользуясь выражением

где tpf – коэффициент Стьюдента при заданной вероятности; f=n-1; S – стандартное отклонение измеряемой величины, рассчитанное для выборочной совокупности из n данных. Доверительную вероятность принимали равной 0,95.

Смотрите также

Получение хлора и щелочи путем электролиза водных растворов хлоридов щелочных металлов. Извлечение ртути
Электролизеры для производства хлора и щелочи, в которых используется ртутная амальгама, находят широкое применение благодаря возможности получения концентрированных растворов щелочи. Однако ...

Разделение смеси бензол – циклогексан – этилбензол – н-пропилбензол экстрактивной ректификацией
Процесс ректификации играет ведущую роль среди процессов разделения промышленных смесей. Большая энергоемкость процесса делает поиск оптимальных схем разделения актуальной задачей химическо ...

Cупрамолекулярная химия
Проанализировано развитие области науки, называемой супрамолекулярной химией. Даны основные определения и понятия этой дисциплины. В историческом контексте рассмотрены исследования, заложивш ...